Privacy Pass: Bypassing Internet Challenges Anonymously

 ·  ☕ 6   ·  ✍️ Techsum

一些私货

为啥读论文儿

  • 真正的一手资料，比书籍更强的时效性和专业性

  • 启发思维和反常理的结论

  • 读书与工作环境的影响

读论文儿的一些方法

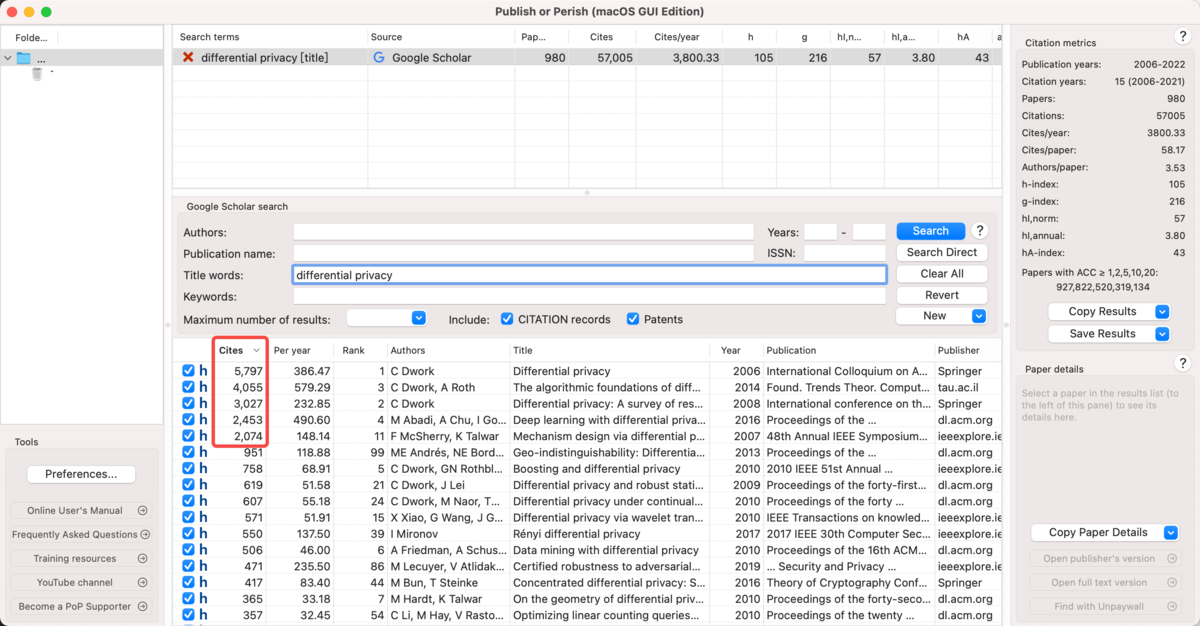
image

image

image

image

image

  • 英语看不懂？chrome插件 划词翻译

image

image

  • 数学符号？。。。无能为力，只能慢慢积累

  • 关键部分：Introduction！

正题：Privacy Pass

原文：https://www.petsymposium.org/2018/files/papers/issue3/popets-2018-0026.pdf

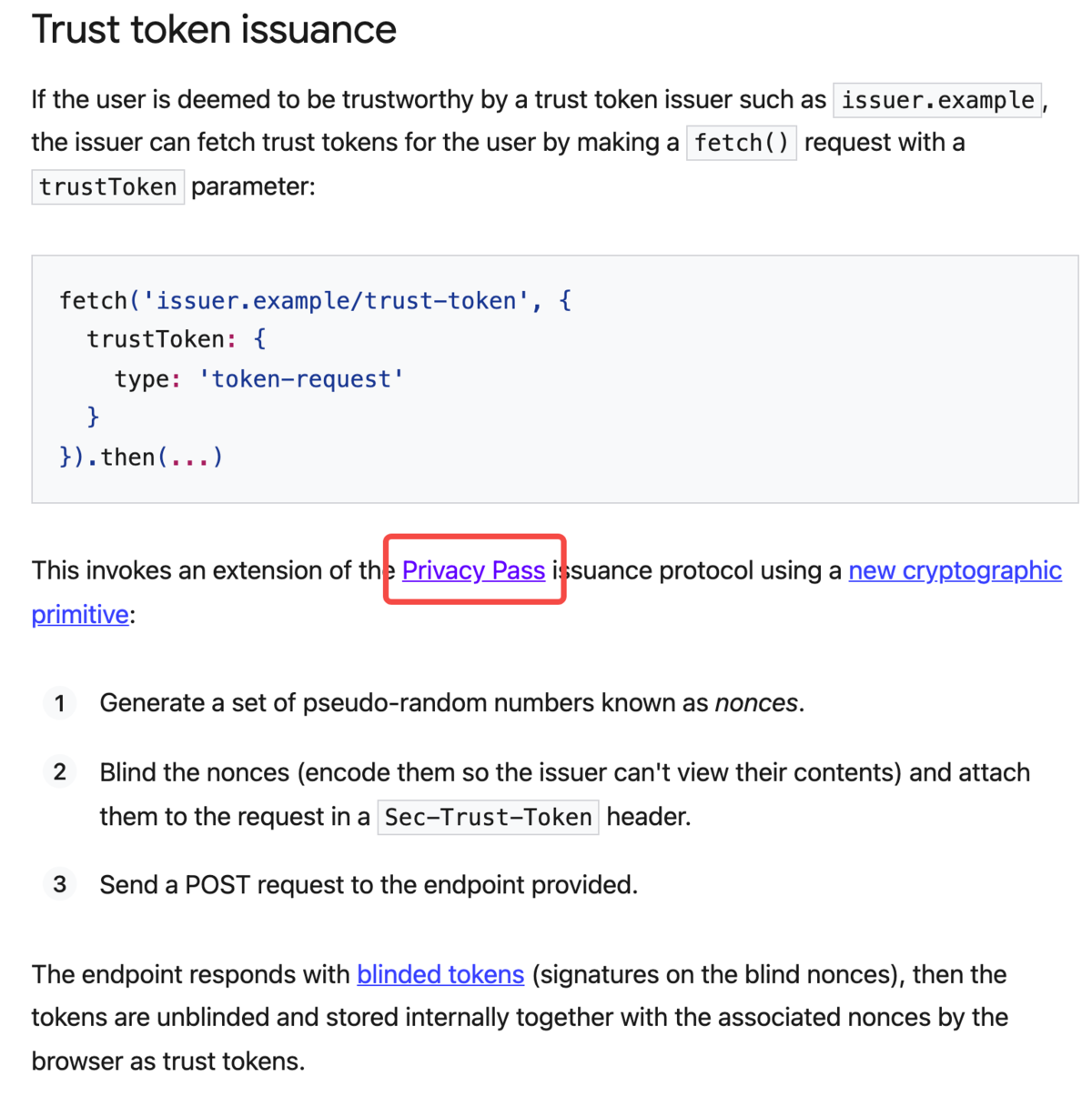
为啥看他

image

  • Privacy Pass拓展在10月发布了v3版本：https://github.com/privacypass/challenge-bypass-extension

  • CloudFlare 作为世界最大的CDN厂商最早开发了Privacy Pass体系，已经使用了三年

  • 优点：

    • 最主要作用：大规模减少网络上的Challenge（人机挑战）的流量

  • 保护用户隐私的token，即服务端验证token时并无法定位具体用户

  • 用户可验证下发token不是被中间人或恶意服务伪造

  • token即使泄露也将快速消费完，无记忆性

  • 缺点：

LET’S DISCUSS

背景知识

一个群儿

群是一个集合，有四个主要性质(封闭性，结合律，单位元，逆元)；但我们只讨论他的一个性质：阶

定义一个群的阶N为：任意群里的一个元素他对自己做N次定义群的运算后会等于他自己，则该群的阶为N

我们不搞抽象的，我们想一个具体的模乘群：$\mathbb{Z}_p = \lbrace 1, 2, …, p-1 \rbrace $, p为质数，其阶就为p

为啥？费马小定理，具体就不证明了：

image

VOPRF

可验证遗忘性伪随机数发生器(Verifiable oblivious pseudorandom function)：用人话说就是就是一个算法协议，他通过一个秘钥K和种子S来产生伪随机数R，而S是由一个消息M产生；该算法虽然产生了R，但他并不知道M是什么（遗忘性），但产生的R是可以验证一定来自该秘钥K产生的（可验证）

零知识证明ZKP

是实现VOPRF可验证性的重点：如何不告诉你秘钥K的值确定产生的伪随机数是来自秘钥K？

阿里巴巴的故事

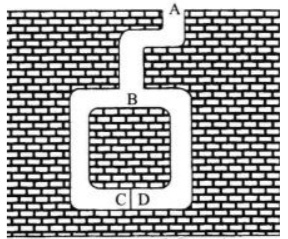
image

阿里巴巴证明自己拥有能打开CD之间的石门的咒语

  • 盗贼站在A，阿里巴巴在B点随机选择前往C或者D
  • 盗贼到B点，随机让阿里巴巴从C或者D走出来，假如他不知道咒语，他也有50%的成功率
  • 重复该实验N次，他连续成功的概率将越来越低，直到到达一个可信的范围

离散对数问题

DH密码协议所依赖的数学难题：

计算$x, y, a \in \mathbb{Z}_p,\ y = a^x\ mod\ p$是简单的，但计算$ x = log_ay$是困难的

消息验证码MAC

用人话说就是A与B共享一个秘钥K，A给B发送一个消息m，同时用这个秘钥K和m进行计算生成一个消息验证码c，将m和c打包发给B。由于B也拥有秘钥K，他可以用相同的算法对收到的消息m’计算消息验证码c’，比较c与c’来判断m’有没有遭到篡改。

比较典型的算法是HMAC与GMAC，由于MAC的前提需要有共享秘钥，GMAC通常与AES结合使用，即AES-GCM模式。

协议分析

image

恐怖吗？我尽量用自己的理解用人话来描述这个协议吧🙄，就不细说具体的严格证明(我也没太看明白，民科罢了)

如何证明我拥有一个离散对数的解

DLEQ(Discrete log equivalence proofs)：有一组公开的数：$(X,\ Y) \in \mathbb{Z}_p, Y = X^k$，阿里巴巴如何证明自己拥有私钥k值？

  1. 盗贼给阿里巴巴一个数$P \in \mathbb{Z}_p$
  2. 阿里巴巴计算$Q = P ^ k$
  3. 阿里巴巴随机生成一个数$t \in \mathbb{Z}_p$
  4. 阿里巴巴计算$A = X ^ t, B = P ^ t, c = Hash(X, Y, P, Q, A, B)$
  5. 阿里巴巴计算$s = t - ck$, 最后把$D_k = (Q, s, c)$给盗贼
  6. 盗贼计算$A’ = Y^cX^s, B’ = P^cQ^s, c’ = Hash(X, Y, P, Q, A’, B’)$
  7. 盗贼判断$c\ ?= c$，若成立，则本次验证通过；且盗贼无法通过$s,c => k$（两个未知数，解不出）；也无法通过$Q => k$（离散对数难题）

证明很简单：

$A’ = Y^cX^s = X^{ck}X^{-ck}X^{t} = X^t = A $

$B’ = Q^cP^s = P^{ck}P^{-ck}P^t = P^t = B$

仅当$s = t - ck$

以上证明形式可以被表述为$D_k \leftarrow \mathsf{DLEQ}_k(X, Y, P, Q)$

推广到发送多个数的乘积，Batch-DLEQ：

该结论可以同时推广到一次通过n个数字$P_i$乘积，一次完成$D_k$的生成:

  1. 验证者随机生成的n个随机数$c_1, c_2, …, c_n $并保存下来，同时发送$ P_1^{c_1} ,P_2^{c_2}, …, P_n^{c_n}$
  2. 证明者计算$\begin{align}
    \lbrace Q_i \rbrace _{i \in [n]} = \lbrace (P_i^{c_i})^k \rbrace ; \\
    M = P_1^{c_1} \cdot P_2^{c_2}…\cdot P_n^{c_n}; \\
    Z = M^k = (P_1^{c_1})^k \cdot (P_2^{c_2})^k…\cdot (P_n^{c_n})^k
    \end{align}$
  3. 把替换成上面的$P,Q$, 完成证明值$\bar{D}_k \leftarrow \mathsf{DLEQ}_k(X, Y, M, Z)$;
  4. 证明者一次把$Q_1, Q_2, … , Q_n, \bar{D}_k$发给验证者，验证者使用DLEQ验证方法完成验证

特点：

  • 效率高，一次完成多次签名，同时可证明
  • Batch-DLEQ的遗忘性：上面$c_1, c_2, …, c_n $可以让证明者并无法获取具体的$Pi$值；此时$c_1, c_2, …, c_n$被称为 盲化因子
  • Batch-DLEQ的可验证性：由DLEQ保证

结论：Batch-DLEQ实现了一个VOPRF

此时由n个随机数组成的DLEQ被称为n-DLEQ，用符号通常表示为(用Pi，Qi来替代了上面的M，Z)
$\bar{D}_k \leftarrow n\text{-}\mathsf{DLEQ}_k(X, Y, \lbrace P_i \rbrace _{i \in [n]}, \lbrace Q_i \rbrace _{i \in [n]})$

Privacy Pass正式协议

整个协议其实分为两个阶段，简单来说就是，Token组签署下发阶段和Token组赎回阶段

Token组签署下发阶段
  1. 服务器发起挑战
  2. 客户端响应挑战，并根据Batch-DLEQ的第一步，随机生成n个随机数$P_1, … ,P_n,$和n个盲化因子$c_1, c_2, …, c_n$, 保存下来，同时完成上面M的计算，将M随挑战响应回复给服务器
  3. 服务器验证挑战，若验证失败则协议结束
  4. 服务器验证挑战成功，计算Z，完成$\bar{D}_k \leftarrow n\text{-}\mathsf{DLEQ}_k(X, Y, \lbrace P_i \rbrace _{i \in [n]}, \lbrace Q_i \rbrace _{i \in [n]})$并下发结果
  5. 客户端验证下发结果，验证该Token的合法性
  6. 去盲化：$\lbrace P_i^k \rbrace _{i \in [n]} = \lbrace Q_i^{1/c_i} \rbrace _{i \in [n]}$, 将$(P_i, P_i^k)$成对保存下来，形成n个Token

这一阶段主要保证了

  • Token的可验证性：Token一定来自可信服务端，无法被中间人伪造
  • Token的隐私性：因为盲化因子的存在，消费Token时并不知道原本的随机数$P_i$，即使服务器记录了这些M也无法追踪客户端

这正是VOPRF的特性

Token组赎回

即客户端消费Token：

  1. 服务器下发挑战，预期的计算结果为$R'$
  2. 客户端取出一个Token，使用一个协议好的哈希函数计算出MAC所使用的key$K = H(P_i, P_i^k)$
  3. 计算挑战结果$R$, 并计算MAC：$C = MAC_{K}(R)$，将两者和$P_i$一起响应给服务端
  4. 服务端先验证$R ?= R’$，若不通过则挑战失败
  5. 服务器取出计算私钥$k$, 计算MAC所需秘钥$K’ = H(P_i, P_i^k)$
  6. 服务器计算对应MAC值，$C’ = MAC_{K’}(R’)$
  7. 挑战响应成功当且仅当$C == C'$

主要优点

  • 一次有感挑战后，可以完成多次无感挑战，提升体验，减少消耗
  • 验证结果可验证，是来自拥有Token的用户
Techsum
Techsum
A useless security engineer/cn:帅华